今日の目的
今日の目標は次のとおりです。「プラス,マイナスはなんのための記号か説明できる」
1-2 が難しいのはなぜか
マイナスのイメージ
マイナスの記号は,数を操作するための記号です。
小学校では「マイナス」のことを,「引く」といいます。「引く」というのは,「取る」というイメージですね。
こういうイメージをもっていると, $1−2$ であるとか, $2−(−5)$ の計算を勉強するときにとまどってしまうでしょう。
例えば, $1−2$ を考えてみましょう。マイナスを「引く」や「取る」というイメージで捉えている場合,困ったことがおきます。2 個から 5 個をとるわけにはいかないからです。
数直線で考える
小学校では,りんごが2個あります。そこにりんごを3個くわえます。りんごは何個になりましたかという具合に,数をものの数として考えていました。小学生の場合は具体的なものをイメージしたほうがわかりやすいので,このような指導がされています。
中学生になっても,数をものの数として考えると, $1−2$ をであるとか, $2−(−5)$が何を表しているのかわからなくなっていまいます。
中学生からは,数を数直線のうえにあるものとしてとらえることが大切です。数直線とは次のように,線のうえに数が並んでいるものと考えてください。
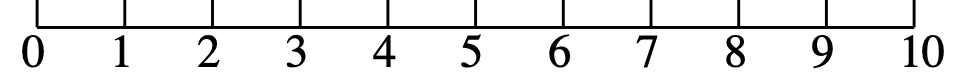
マイナスの意味
マイナスは,この数直線の上の位置を操作するためにあります。マイナスは「戻る」と考えます。
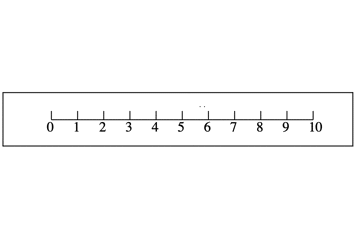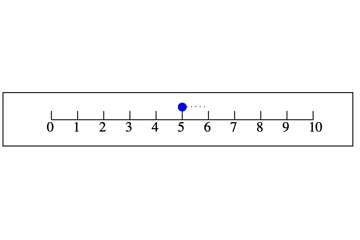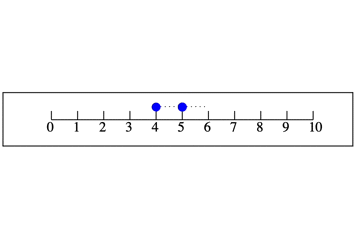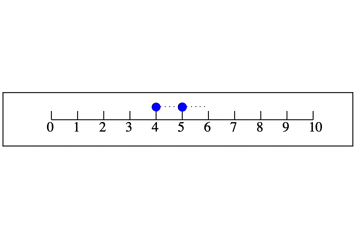
想像してください。あなたが今,数直線の6の位置にいるとしましょう。この数直線の上では「進む」とは右に進むこと,「戻る」とは左に進むことだと考えてください。左を進行方向だとすると,左に行くこととは「進む」,右に行くことは「戻る」となります。
数直線の6にいるとき,2つ「戻る」ことを,式で表すと, $6−2$ と書けます。
プラスの意味
マイナスが戻るであれば,プラスは進むです。次のようなイメージです。
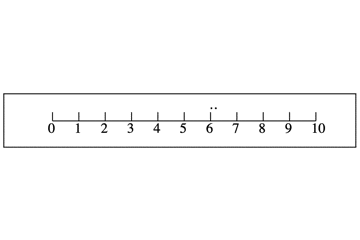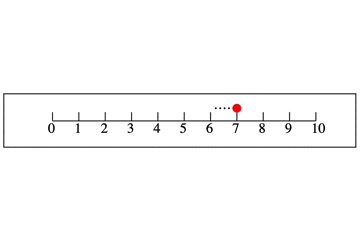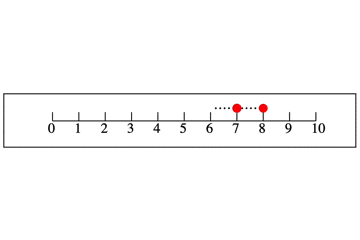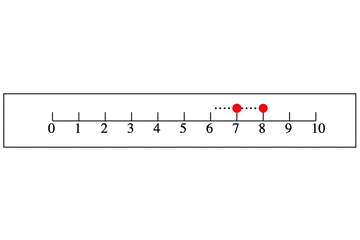
1-2を考える
これまでは,0 以上の数直線を考えていました。これからは,マイナスも含めた垂直線で考えてみましょう。
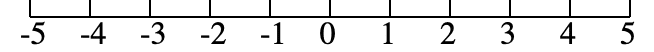
それでは, $1−2$ を考えます。あなたが数直線の1のところにいるとしましょう。
$1−2$ の $−2$ とは2つ「戻る」ということです。数直線の1のところから,左に2戻るということです。
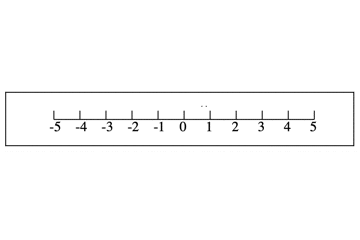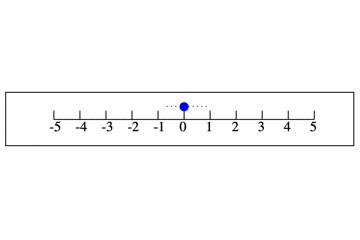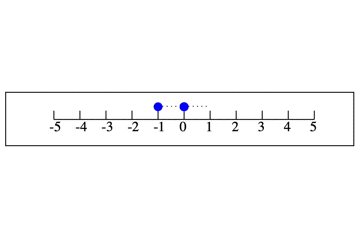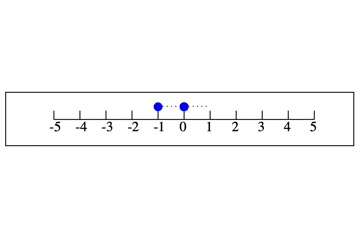
2戻ると今どこにいますか? -1 ですね。
まとめ
数直線で考えると数直線で考えると, $1−2$ のように結果がマイナスになる式の理解も簡単になります。今日の勉強の目的は「プラス,マイナスはなんのための記号か説明できる」ことにありました。
マイナスの操作を説明してみてください。
どうですか?できましたか?
練習
問題1
2−7
問題2
1−4
問題3
6−9
問題4
1−3
問題5
3−8
問題6
2−5
問題7
4−6
問題8
5−9
答え
問題1
2−7=−5
問題2
1−4=−3
問題3
6−9=−3
問題4
1−3=−2
問題5
3−8=−5
問題6
2−5=−3
問題7
4−6=−2
問題8
5−9=−4
おすすめの本
エンツェンスベルガー (著)「普及版 数の悪魔―算数・数学が楽しくなる12夜」(晶文社) [Amazon]
数学が嫌いな男の子の夢のなかに現れた,数の悪魔。夢のなかで男の子は悪魔と一緒に数の神秘にふれる。「数学・数学が楽しくなる12夜」とサブタイトルがついています。たぶん,本当にそうなると思います。だまされたと思って読んでみてはいかがでしょう?



コメント